Math

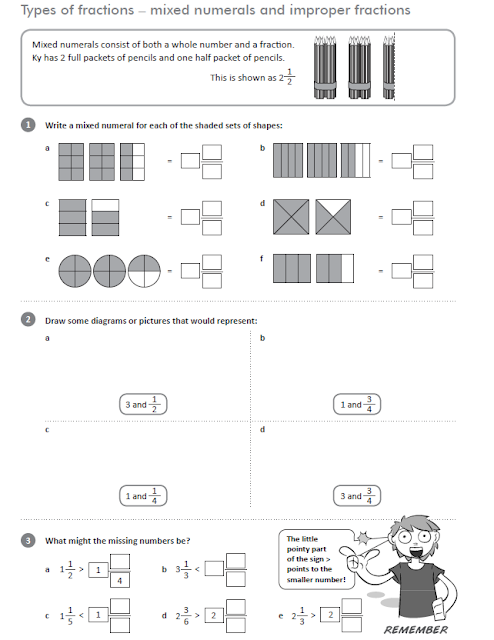
Our mental math strategy today was making magic tens. There are a few ways to make magic tens. Use the strategy that you find the easiest, but challenge yourself to use more than one strategy. For example:

38 + 45 = ?

If we use the "give and take" method, we add 2 to 38 and take 2 away from 45 so our new question is: 40 + 43 = ? It's easy to add on from ten, 40 + 40 + 3 = 83

If you had the question 67 + 23= ? you could solve it using the "give and take" method or you could see a magic ten in the ones place. 7+3 = 10 and 60 + 20 = 80 so the answer is 80 + 10 = 90.

Try these strategies for the questions below:
29 + 36
52 + 28
37 + 37

Today we also discussed different  ways to represents numbers. Using 26 812...

Standard Form: 26 812
Expanded form numbers (numerals) : 20 000 + 6000 + 800 + 10 + 2
Expanded from words (and numbers): 2 ten thousands + 6 thousands  + 8 hundreds + 1 ten + 2 ones
On a place value chart:

Ten Thousands	Thousands	Hundreds	Tens	Ones
2	6	8	1	2

Base-Ten Blocks:

How it is read:

twenty-six thousand eight hundred twelve

Please play the game after you finish your homework.

Literacy

Today we shared the story "Dictionary Dave" and practiced check for understanding. Remember when you check for understanding you do NOT retell the story, you summarize or pick out the most important idea or ideas.

Practice reading your book fluency out loud. Check for understanding as your read. Make sure yo know how to read all the words. Tomorrow you will be reading your book with your group. You will have a short quiz (multiple choice) after your group is finished reading. You may use the book to answer the questions.

PLEASE RETURN THE BOOK. YOU WILL NOT HAVE A BOOK TO READ IF YOU LEAVE IT AT HOME!

Science

On this beautiful day we went to explore the habitats around our school. You should have listed the living and non-living parts of area you chose to explore. If it is living, it is either a plant or animal. Thursday we will be looking at the photographs and notes you took on each area.

We saw lots of these in the tall grass. Can you identify them?

Kagan / Collaborative Work 

Share with a parent the name you chose for your group. Explain how the name was chosen. It might take me a few days to learning all the creative names!

Reminders:

Outstanding forms / $10 for Agenda

Back to School BBQ tomorrow (Wednesday 4:30 - 6:00 pm)

Cross country practice tomorrow

Happy 6th Week of Summer!

Some thinking questions ......

What real life situation might the number $25 000 describe?
Hint: Think of people or money.

You read a five-digit number. How many words might you say? Think of all the possibilities. Which numbers use the fewest words? Which numbers use the most words?

What are all the ways you could describe 23 117. Think of all the forms of a number (e.g. expanded form (numbers and words), base-ten blocks, words etc.).

You use three words to write a four-digit number on a cheque. List four numbers you could be writing. Then write the numbers in words. What do you notice about the numbers that you wrote?

If a number is closer to 22 000 than 23 000, what do you know about the number?

A hockey arena holds about 13 244 people. About how many games would it have to sell out for there to be 100 000 sold?

About how long would it take to travel 100 000 mm?
Hint: 1000 mm = 1 m     1 km = 1000 m   Average walking speed is about 5 km per hour

Model two improper fractions with a denominator of 10. How are they the same? How are they different?

Is there a fraction between 40/100 and 5/10? Explain your answer.
Hint: Find an equivalent fraction for 5/10

Write a sentence that includes: 2/3, 1/2 part, greater.

Pencils come in packs of 10. You have __.1 packs of pencils. How many pencils might you have? How many could you not have?

__.__ and __ __.__ are close together. What could go in the blanks?

A fraction and decimal are quite close together on a number line. What might the two numbers be?

Which is greater:  __ __ __ or __ __ . __? Does it depend what is in the blanks?

I'll post possible solutions next week. THINK HARD! Use all the different kinds of problem solving strategies.

Happy 5th Week of Summer!

My computer survived the virus attack. Be very weary of unknown sites..
Let's continue with fractions and decimals.....
Equivalent fractions have the same value, that is, are the same amount. They just have a different denominator. They are divided into a different number of parts or pieces.

Go back to past posts to review how to change from improper fractions to mixed numbers. Remember a mixed number or improper fraction show amounts that are equal to or greater than 1 whole.

So far, everything should sound pretty familiar. Putting a fraction into LOWEST TERMS is new. To put a fraction into lowest terms, we must find the GREATEST OR HIGHEST COMMON FACTOR (GCF or HCF). This is where knowledge of your division and multiplication facts is very important. You have to find the biggest number that divides evenly into both the numerator and the denominator.
For example, let's look at the fraction 4/6. What is the biggest number that divide evenly into both 4 and 6? To find this, list all the factors of 4 and 6 and look at the largest one they have in common.

1 x 4 = 4 and 2 x 2 = 4 so the factors of 4 are 1, 2, 4
1 x 6 = 6 and 2 x 3 = 6 so the factors of 6 are 1, 2, 3, 6

The largest factor they have in common is 2. If you divide the numerator and denominator of 4/6 by 2 we get 2/3. 4/6 in lowest terms is 2/3.
Watch the video below to help understand:
https://www.youtube.com/watch?v=AtBUQH8Tkqc&t=14s

 

 



 

A little game to play:

http://www.sheppardsoftware.com/mathgames/fractions/mathman_reduce_fractions.htm

 

Next week will be my last post. I have to get ready for next year! I opened all the windows to Mathletics so feel free to practice, practice, practice!!





Hi everyone. My computer has a virus and is being repaired. I'll post as soon as I can. 😀

Happy 4th Week of Summer!

Continuing with fractions from last week. We can express fractions greater than 1 as mixed numbers or improper fractions.


Remember how to change a mixed number to an improper fraction:

Remember how to change an improper fraction to a mixed number:

Here's some practice:

 

 

Watch the video to see the link between fractions and decimals:

https://www.youtube.com/watch?v=Mst8iZjIpFE&t=9s



It's very important that you are able to perform long division to convert fractions to decimals. After a while, you'll remember the decimal of common fractions. These are ones that you should learn:

To change a decimal to a percent, you multiply by 100 or move the decimal two place values to the right.
In math, we often express decimals or fractions as a percent. Percent means out of 100. Sometimes it's easier to visualize the amount out of 100. For example, if 3/4 of the class memorized their multiplication facts, 3/4 is 0.75. But 0.75 is 75%. So if there were 100 students, 75 would know their multiplication facts. Percentages are a universal way to express fractions or decimals. Look around the grocery store or mall. Labels on food tell us the percentage of a nutrient that is in the food. Clothing store use percentages to tell the discounted price... 30%, 40%, 50%... off.

Watch the video about percentages:
https://www.youtube.com/watch?v=JeVSmq1Nrpw

Can you be a millionaire? Try the game below. Remember to change a decimal to a percent move the decimal two places the right. Yes, percentages can be greater than 100 if the decimal or fraction is greater than 1. Good luck..... until next week.
http://www.math-play.com/Changing-Fractions-and-Decimals-to-Percents/changing-fractions-and-decimals-to-percents-millionaire-game.html
DON'T FORGET TO GO ON MATHLETICS!

Happy Third Week of Summer!

Let's look at fractions. Recall:

Try these:

A little trickier is fraction of an amount. To find the fraction of an amount we have to remember that the fraction line also means division. So what is 1/4 of 20? It is 20 divided by 4 which is 5. To show this in pictures, you would draw 20 circles or x's and put them into 4 groups (quarters). How many in each group? There would be 5.

XXXXX
XXXXX
XXXXX
XXXXX

Fraction game:
http://www.sheppardsoftware.com/mathgames/fractions/memory_fractions3.htm

Here's some practice with main idea:
https://www.ixl.com/ela/grade-5/determine-the-main-idea
https://www.quia.com/pop/120023.html?AP_rand=169119093
Don't forget to practice using Mathletics!

Happy Second Week of Summer!
Some place value review...

 

Renaming numbers is important to understanding place value. For example, how many different ways can you express 48 295? You can use...

 48 295 ones
4 ten thousands + 82 hundreds + 95 ones
48 thousands + 295 ones
482 hundreds + 9 tens + 5 ones
4829 tens + 5 ones
There are more....

Being able to rename numbers also helps you divide and multiply by 10, 100, 1000, etc.

Try this one:

Please check out the grammar games below. You can try all grades but make sure you understand the skills to the end of the grade five.
https://www.eduplace.com/kids/hme/k_5/grammar/

A little bit of Canadian geography:
https://www.canadiangeographic.ca/sites/cgcorp/files/images/web_articles/kids-games/flash/games/storepuzzle.html